データを代表する値として、もっとも使用されるのが「平均値(mean)」です。しかし、平均値がいつも代表値として適しているとは限りません。例えば、外れ値がある場合や分布が非対称なデータでは「中央値(median)」の方が適当です。
また、データの特徴として散らばり具合も把握する必要があります。そのために「標準偏差(standard deviation)」が用いられます。
このようにデータの特徴を知るには、「平均値」「中央値」「標準偏差」の3つが最低限必要です。しかし、省庁公開のデータ等で3つの値全てが明記されていることは多くありません。そのような時に、公開されているデータから何らかの方法で推定できると助かります。
そこで、今回は度数分布表(ヒストグラム)だけでも入手できた時に、そこから3つの値を推定するPythonプログラムを紹介します。
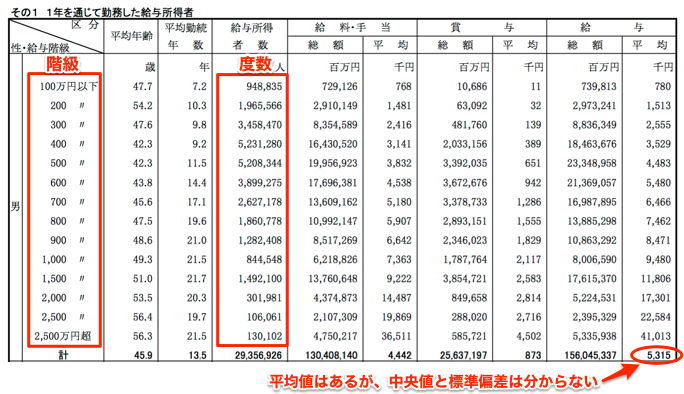
例えば、以下の給与統計では「平均値」は分かりますが、「中央値」「標準偏差」が不明です。このような場合でも「階級」と「度数」がわかれば、それだけで推定できます。
平成29年分 民間給与実態統計調査(国税庁) 第3表 給与階級別の総括表より
どうしても「平均値」が重視されがちですが、「中央値」と「標準偏差」もあればもっと踏み込んだ議論が可能になります。ぜひ今回紹介するプログラムを活用してください。
ヒストグラムだけしか入手できない場合
ヒストグラムしか手元にない場合には、ヒストグラムを読み取り度数分布表を作成することで、今回の方法を利用できます。
本記事の目次
使用するPythonライブラリ
今回は、Pythonにおいて数値計算を行うのに非常に便利なNumPyと呼ばれるライブラリを利用します。NumPyを用いると、配列同士の計算が簡単になるだけでなく、テスト用の度数分布表を算出するのにも活用できます。
NumPyのインストール方法は以下の記事を参考にしてください。
プログラム
以下にPythonプログラムのソースコードを示します。
# stat_index.py
import numpy as np
def from_freq(bins: np.array, y: np.array):
"""
度数分布表から統計値を推定
:param bins: 階級の境界
:param y: 度数
:return: 推定値(平均値、中央値、標準偏差)
"""
x = 0.5 * (bins[:-1] + bins[1:]) # 階級値(階級の中心)
n = np.sum(y)
avg = np.sum(x * y) / n
sdv = np.sqrt(np.sum(np.power(x - avg, 2) * y) / n)
mi, mr = search_med_contain(y)
med = bins[mi] + (bins[mi + 1] - bins[mi]) * mr
return avg, med, sdv
def search_med_contain(y):
"""中央値を含む階級を探す
"""
center = int((np.sum(y) + 1) / 2)
val = 0
for i, v in enumerate(y):
val += v
if val > center:
return i, (center - (val - v)) / v
原理はとても単純です。全データの個々の値は不明で、分かっているのは度数分布表だけです。そこで、ある階級に含まれるデータの値は、すべて「階級値(階級の中心)」であると仮定します。つまり、階級「100〜200」の度数が「450」の場合、値=150のデータが450個あると考えます。
このようにすれば、全データの個々の値を仮定できるので「平均値」と「標準偏差」を計算できます。「中央値」は、まず度数の合計の1/2を含む階級を求めます。その階級の幅を度数で等分し、度数の合計の1/2の位置に相当する値を計算します。
計算例
前述の国税庁公開の「給与階級別の総括表」のデータを用いて計算してみます。上記のプログラムをモジュールとして読み込んで利用します。なお、階級の両端の境界値(56と5700)は、それぞれの階級内の平均値から適当な値を逆算しています。
# stat_index_income.py
import numpy as np
import stat_index
bins = [56, 100, 200, 300, 400, 500, 600, 700, 800, 900, 1000, 1500,
2000, 2500, 5700]
values = [948835, 1965566, 3458470, 5231280, 5208344, 3899275, 2627178,
1860778, 1282408, 844548, 1492100, 301981, 106061, 130102]
results = stat_index.from_freq(np.array(bins), np.array(values))
print(" Mean ", " Median ", " Std ")
print(" ".join(["{:10.5f}".format(x) for x in results]))
プログラムを実行すると以下の結果が出力されます。
Mean Median Std
535.27503 459.02667 393.92267
平均値(Mean)=535万円、中央値(Median)=459万円、標準偏差(Std)=393万円が推定されます。変動係数(Std/Mean)を計算すると0.74とばらつきが大きいのがわかります(日本はまだ良い方かもしれませんが…)。
H29年度 給与所得の基本統計量(男子)
| データ | 推定 | |||
|---|---|---|---|---|
| 平均値(万円) | 平均値(万円) | 中央値(万円) | 標準偏差(万円) | 変動係数 |
| 531.5 | 535.3 | 459.0 | 393.9 | 0.74 |
テスト計算
上記の計算は平均値しか正解が分からないので、妥当性を評価できません。そこで、NumPyの乱数生成機能を用いて、「正規分布」と「F分布」に基づくデータを作成して検証します。
# stat_index_test.py
import numpy as np
import stat_index
def test_from_freq(values, bins_num):
"""from_freq()関数のテスト用
"""
y, bins = np.histogram(values, bins=bins_num)
est_idx = stat_index.from_freq(bins, y)
# 真値
true_idx = np.mean(values), np.median(values), np.std(values)
# 誤差
err = (np.array(est_idx) - np.array(true_idx)) / np.array(true_idx)
print("This Method : ", " ".join("{:10.5f}".format(v) for v in est_idx))
print("True Value : ", " ".join("{:10.5f}".format(v) for v in true_idx))
print("Error(%) : ", " ".join("{:10.3f}".format(v * 100) for v in err))
print("テスト:正規分布データ")
vn = np.random.normal(50, 10, 1000)
test_from_freq(vn, 10)
print("テスト:F分布データ")
vf = np.random.f(20, 30, size=1000) * 10
test_from_freq(vf, 10)
以下に2回テストを実施した結果を示します。今回の結果では、標準偏差で最も誤差が生じていますが、概ね3%以内の誤差で推定できています。
テスト1回目
テスト:正規分布データ
This Method : 49.39314 49.01689 10.27775
True Value : 49.31025 48.72129 10.05117
Error(%) : 0.168 0.607 2.254
テスト:F分布データ
This Method : 10.50253 9.85903 4.34246
True Value : 10.52191 9.89487 4.23108
Error(%) : -0.184 -0.362 2.633
テスト2回目
テスト:正規分布データ
This Method : 49.58010 49.20975 9.86521
True Value : 49.61634 49.28041 9.67007
Error(%) : -0.073 -0.143 2.018
テスト:F分布データ
This Method : 10.39390 9.84479 4.48441
True Value : 10.46736 9.80710 4.41301
Error(%) : -0.702 0.384 1.618
最後に
平均値は便利ですが万能ではありません。平均値だけで議論してしまうと現状との乖離を招くことになります。その代表例が2019年6月に話題となった「老後2000万円」問題です。
これも「平均値=平均像」という強引な理論展開が騒動の要因の1つであると思われます。もっと丁寧にデータを扱うためにも、今回紹介したプログラムが十分活用できると考えます。
