金利の計算方法には「単利」と「複利」の2つの種類があります。「単利」は元本に対してのみ利息がつきますが、「複利」は生じた利息を次期の元本に繰り入れします。
今回は、年ごとの定額積立の元利合計の推移を、単利と複利の2通りで計算し、グラフで可視化するPythonプログラムを作成します。例えば、年利3%の金融商品を毎年30万円ずつ40年間積み立てた場合は、以下のようなグラフを出力します。
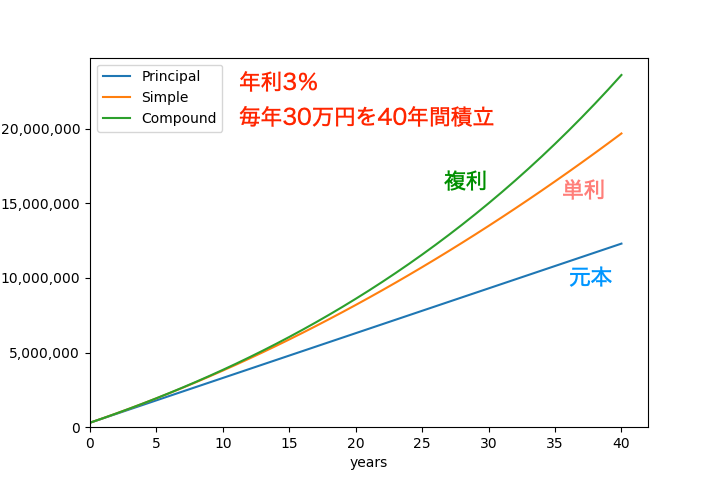
本サイトのPython入門と同じく「Webブラウザで実行できるPython」を利用しているので、すぐに実行できます。
なお、本記事での計算は、あくまでも金利の計算方法を説明するための単純な例です。一般にかかる税や手数料は一切考慮しておらず、実際とは異なります。実際の資産運用や投資判断にあたっては、必ずご自身の責任において判断してください。
本ページのPython実行環境について
- ブラウザでPythonを実行できるPyodide 0.25.0(Python 3.11.3)を利用しています。
- 本ページのコードを試行する用途のみにご利用ください(input()など本ページで使用していない機能には動作しないものがあります)。
Python実行環境 ロード中… しばらくお待ちください
Pythonプログラム
以下のプログラムは「年利3%」の金融商品を1年毎に「30万円」ずつ「40年間」積み立てた場合に、元利合計がいくらになるかを「単利」と「複利」の2通りで計算し、推移を可視化します。
以下の実行ボタンを押すと結果とグラフを出力できます。以下のコードは編集可能なので、年利は変数rate、運用年数は変数yearsを書き換えると変更した結果を計算できます。
なお、今回の計算では40年以降も積立を継続するものとします。そのため、40年目も新規の積立元本を加えた金額になります。
解説
上記のプログラムのポイントは、単利計算(27行目)と複利計算(29行目)のコードです。このコードを理解しやすくするために、3年間だけ運用した時点の積立状況を例に考えてみます。
単利計算
「単利」で3年間運用した時点の積立
| 1口目 | 2口目 | 3口目 | 4口目 | |
|---|---|---|---|---|
| 0年目 | 300,000 | |||
| 1年目 | 309,000 | 300,000 | ||
| 2年目 | 318,000 | 309,000 | 300,000 | |
| 3年目 | 327,000 | 318,000 | 309,000 | 300,000 |
単利で運用した場合、元利合計は上の表ように積み立てられます。
ここで、3年目の元利合計に着目すると、以下のように2年目の元利合計に「1口目の単利3年目の運用結果」を加えた値になります。
3年目の元利合計 = 2年目の元利合計 + 1口目の単利3年目の運用結果
= 2年目の元利合計 + 300000 * ( 1 + 0.03 * 3)
= 2年目の元利合計 + 327000
そのため、コードでは年ごとにループさせて、1口目のi年目の運用結果を前年の元利合計に、simple += amount * (1 + rate * i / 100)で順次加えて計算します。
複利計算
「複利」で3年間運用した時点の積立
| 1口目 | 2口目 | 3口目 | 4口目 | |
|---|---|---|---|---|
| 0年目 | 300,000 | |||
| 1年目 | 309,000 | 300,000 | ||
| 2年目 | 318,270 | 309,000 | 300,000 | |
| 3年目 | 327,818 | 318,270 | 309,000 | 300,000 |
複利で運用した場合、元利合計は上の表ように積み立てられます。
ここで、3年目の元利合計に着目すると、以下のように2年目の元利合計に「1口目の複利3年目の運用結果」を加えた値になります。
3年目の元利合計 = 2年目の元利合計 + 1口目の複利3年目の運用結果
= 2年目の元利合計 + 300000 * ( 1 + 0.03 )**3
= 2年目の元利合計 + 327818
そのため、コードでは年ごとにループさせて、1口目のi年目の運用結果を前年の元利合計に、compound += amount * (1 + rate / 100) ** iで順次加えて計算します。
参考書籍
金利の計算に関しては以下の書籍がとてもわかりやすくおすすめです。本記事の執筆にあたっても参考にさせていただきました。
