年金は本当に「分かり難いことが多い」です。仕組み、実態、いくら貰えるのかなどを理解することはとても難しいです。そのため話題になるたびに不安を感じるのも無理がありません。
年金の仕組みは非常に難解です。弊社も勉強しようとしましたが、無理と判断しました(まず用語がさっぱり頭に入りません)。しかし、実態についてならば、統計データが厚生労働省から公開されているので何とかなりそうです。
そこで、Pythonを駆使して年金の実態について調べてみました。今回は年金月額別の受給権者数のデータを分析して、現在どのくらいの月額を貰えているのかを様々な角度から把握します。
結論としては、年金受給額はバラツキ(格差)が全般に小さくなる傾向にあります。しかし、男女間の差は未だ大きく、そこが一番の問題であることが分かります。
エクセルでも同様の分析は可能ですが、Pythonならばエクセルのデータを読み込んでグラフ化だけをプログラムにできます。ソースコードも記載していますので、Pythonを使ったデータ分析例としても活用してください。
本記事の目次
使用データ
データには、厚生労働省が年金事業の状況を把握し、適正な運営をはかるための基礎資料としている「厚生年金保険・国民年金事業統計」を用いました。今回は以下の政府統計ポータルサイト(e-Stat)から、平成27、28、29年度のデータをダウンロードして使用しました。
各年度のデータセットからは、以下のように各種整理されたデータをエクセルファイルでダウンロードできます。今回は「厚生年金保険(第1号) 年金月額階級別受給権者数」のエクセルファイルをダウンロードして利用しました。
今回使用したエクセルファイルは以下の3つです。
厚年12表_h27年度.xlsx厚年12表_h28年度.xlsx厚年12表_h29年度.xlsx
厚生年金保険(第1号)とは
公務員、私立教員以外の厚生年金の被保険者のことです。つまり、民間企業の会社員が該当します。
データファイルの内容
上記でダウンロードした「年金月額階級別受給権者数のエクセルファイル」は以下のような中身になっています。ファイルは厚年12表_h27年度.xlsxです。
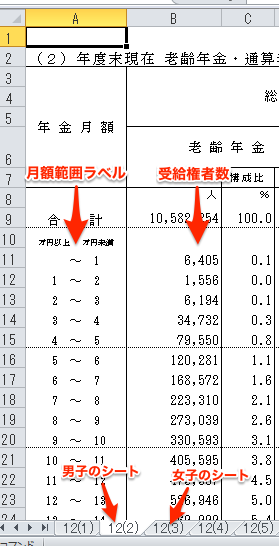
上図のように月額範囲ごとに受給権者数が集計されています。男子と女子はシートが分かれています。それぞれシート名は、男子=「12(2)」と女子=「12(3)」で固定されています。
各データファイルから読み取った年度ごとの受給権者数と平均年金月額は以下の通りです。なお、ここでの年金月額には基礎年金月額も含まれています。
厚生年金保険(第1号)の受給権者数
| 年度 | 全体(人) | 男子(人) | 女子(人) |
|---|---|---|---|
| H27 | 15,684,112 | 10,582,254 | 5,101,858 |
| H28 | 15,687,976 | 10,497,777 | 5,190,199 |
| H29 | 15,899,722 | 10,629,255 | 5,270,467 |
厚生年金保険(第1号)の平均年金月額
| 年度 | 全体(円) | 男子(円) | 女子(円) |
|---|---|---|---|
| H27 | 145,305 | 166,120 | 102,131 |
| H28 | 145,638 | 166,863 | 102,708 |
| H29 | 144,903 | 165,668 | 103,026 |
Pythonプログラミング
今回は年金月額階級別の受給権者数について、「基本統計量」、「分布状況」、「性別による比較」、「年度による比較」をPythonプログラミングで把握します。
プログラミングに際しては、データ分析に用いる主要なPythonライブラリであるNumPy、pandas、Matplotlibを利用します。インストール方法は以下の記事を参考にしてください。
データの読み込みプログラム
上記のエクセルファイルから、以下のコードでpandasを用いて「月額範囲のラベル」と「受給権者数」の部分を読み取ります。男子と女子はシートが分かれているので、それぞれ別に読み取ります。
# nenkin_reader.py
import pandas as pd
def read_xl_table12(file_path):
"""
年金事業統計 年金月額階級別受給権者数(第12表)の読み込み
:param file_path: xlsxファイルのパス
:return: (月額範囲ラベル, 男子受給権者数, 女子受給権者数)
"""
sheet_names = {"men": "12(2)", "women": "12(3)"}
df = pd.read_excel(file_path,
sheet_name=list(sheet_names.values()),
header=None,
usecols=[0, 1], names=["x", "y"],
skiprows=10, nrows=31,
dtype={0: str, 1: int})
data_men = df[sheet_names["men"]]
data_women = df[sheet_names["women"]]
labels = [x.replace("\u3000", "").replace("\n", "").strip()
for x in data_men["x"].to_list()]
return labels, data_men["y"].to_list(), data_women["y"].to_list()
基本統計量
今回のデータでは、平均値は算出されていますが、中央値と標準偏差の値を見つけることができませんでした。そこで、以下のプログラムを利用して度数分布表から推定しました。
推定した統計量は以下の通りです。
厚生年金保険(第1号)の年金月額統計量【男子】
| 年度 | データ | 推定 | |||
|---|---|---|---|---|---|
| 平均値(円) | 平均値(円) | 中央値(円) | 標準偏差(円) | 変動係数 | |
| H27 | 166,120 | 166,030 | 170,697 | 51,609 | 0.311 |
| H28 | 166,863 | 166,776 | 171,191 | 50,287 | 0.302 |
| H29 | 165,668 | 165,594 | 170,163 | 50,108 | 0.303 |
厚生年金保険(第1号)の年金月額統計量【女子】
| 年度 | データ | 推定 | |||
|---|---|---|---|---|---|
| 平均値(円) | 平均値(円) | 中央値(円) | 標準偏差(円) | 変動係数 | |
| H27 | 102,131 | 102,128 | 98,773 | 35,885 | 0.351 |
| H28 | 102,708 | 102,704 | 99,183 | 35,301 | 0.344 |
| H29 | 103,026 | 103,027 | 99,495 | 34,969 | 0.339 |
標準偏差は男子で約5万円、女子で約3.5万円ですが、僅かずつ小さくなる傾向があります。変動係数も小さくなってきています。つまり、この3年分の推移だけからですが、バラツキ小さくなる傾向が見受けられます。
所得よりも年金はバラツキ(格差)が抑えられています
以前の記事で所得の統計量を推定した結果では、男子の所得の変動係数は0.74でした。それが年金では0.3程度に抑えられています。この結果だけから見れば、所得の格差は年金では緩和されていると言えます。
プログラム
エクセルファイル読み込みプログラムnenkin_reader.pyと統計量推定プログラムstat_index.pyをモジュールとして利用しています。
# nenkin_stat.py
import numpy as np
import nenkin_reader
import stat_index
def calc_index(x_labels, y_values):
xi = [int(x.split("~")[0]) for x in x_labels[1:]]
xi = [0] + xi + [31]
xi = np.array(xi) * 10000
yi = np.array(y_values)
return stat_index.from_freq(xi, yi)
def index_to_str(mean, med, std):
return ("{:8d}".format(int(mean)),
"{:8d}".format(int(med)),
"{:8d}".format(int(std)),
"{:8.3f}".format(std / mean))
data27 = nenkin_reader.read_xl_table12("./Data/厚年12表_h27年度.xlsx")
data28 = nenkin_reader.read_xl_table12("./Data/厚年12表_h28年度.xlsx")
data29 = nenkin_reader.read_xl_table12("./Data/厚年12表_h29年度.xlsx")
# 男子
stat27_men = calc_index(data27[0], data27[1])
stat28_men = calc_index(data28[0], data28[1])
stat29_men = calc_index(data29[0], data29[1])
print("### 男子 ###")
print("年度 ", "平均値 ", "中央値 ", "標準偏差 ", "変動係数 ")
print("H27 ", " ".join(index_to_str(*stat27_men)))
print("H28 ", " ".join(index_to_str(*stat28_men)))
print("H29 ", " ".join(index_to_str(*stat29_men)))
# 女子
stat27_women = calc_index(data27[0], data27[2])
stat28_women = calc_index(data28[0], data28[2])
stat29_women = calc_index(data29[0], data29[2])
print("### 女子 ###")
print("年度 ", "平均値 ", "中央値 ", "標準偏差 ", "変動係数 ")
print("H27 ", " ".join(index_to_str(*stat27_women)))
print("H28 ", " ".join(index_to_str(*stat28_women)))
print("H29 ", " ".join(index_to_str(*stat29_women)))
分布状況
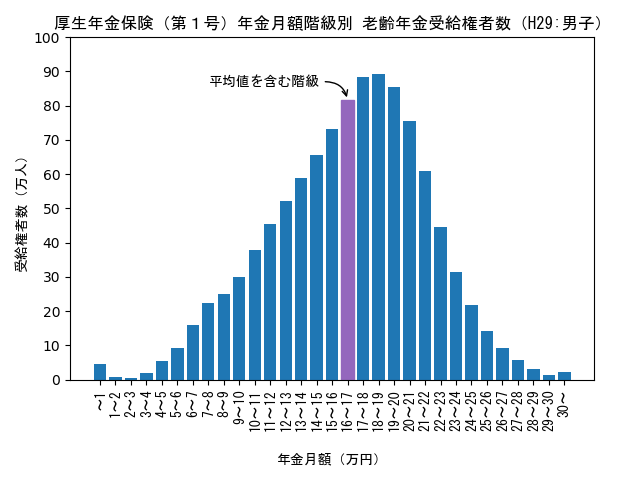
H29年度の男子と女子の年金受給権者数を月額階級ごとにグラフで表すと以下のようになります。
男子の最頻値(モード)は18.5万円になります。平均値は16.6万円、中央値は17万円なので「平均値 < 中央値 < 最頻値」の関係になります。グラフから分かるように、山の左側(最頻値よりも月額が少ない範囲)で傾斜が緩くなっています。
女子の最頻値(モード)は9.5万円になります。平均値は10.3万円、中央値は9.9万円なので「最頻値 < 中央値 < 平均値」の関係になります。グラフから分かるように、山の右側(最頻値よりも月額が多い範囲)で傾斜が緩くなっています。
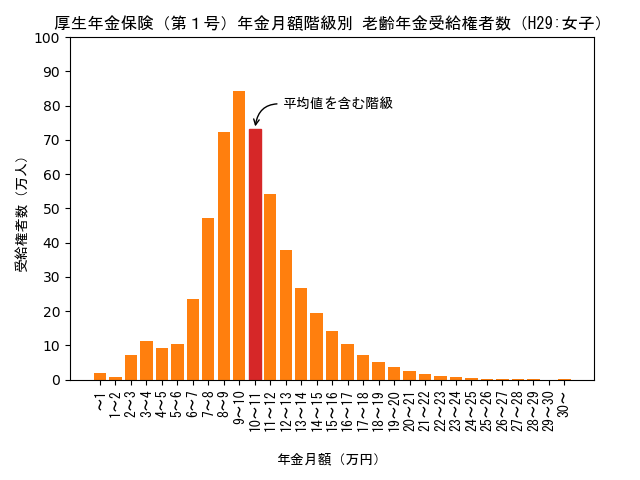
男子と女子では平均値、中央値、最頻値の大小関係が全く逆になります。これは、被保険期間が男子では定年まで一様であるのに対して、女子は一様でないことに起因していると推測されます。
プログラム
Matplotlibを用いて棒グラフを作成しています。作成したグラフはPNG形式の画像で保存します。
# nenkin_dist.py
import numpy as np
from matplotlib import pyplot as plt
import nenkin_reader
TITLE = "厚生年金保険(第1号)年金月額階級別 老齢年金受給権者数"
FONT_NAME = "MS Gothic"
def draw_bar(x_labels, y_values, color):
"""棒グラフ作成
"""
x_ticks = np.arange(len(x_labels))
figure, axis = plt.subplots()
axis.bar(x_ticks, y_values, color=color)
set_axis(axis, x_labels)
return figure, axis
def set_axis(axis, x_labels):
"""軸設定
"""
x_ticks = np.arange(len(x_labels))
y_ticks = np.arange(0, 1000001, 100000)
y_ticklabels = np.arange(0, 101, 10)
axis.set_yticks(y_ticks)
axis.set_yticklabels(y_ticklabels)
axis.set_ylabel("受給権者数(万人)", fontname=FONT_NAME)
axis.set_xticks(x_ticks)
axis.set_xticklabels(x_labels, rotation=90, fontname=FONT_NAME)
axis.set_xlabel("年金月額(万円)", fontname=FONT_NAME, labelpad=15)
if __name__ == '__main__':
data29 = nenkin_reader.read_xl_table12("./Data/厚年12表_h29年度.xlsx")
# 分布状況
fig, ax = draw_bar(data29[0], data29[1], "C0")
ax.set_title(TITLE + "(H29:男子)", fontname=FONT_NAME)
ano_x = data29[0].index("16~17")
ano_y = data29[1][ano_x]
ax.annotate("平均値を含む階級",
xy=(ano_x, ano_y), xycoords="data",
textcoords="offset points", xytext=(-100, 10),
arrowprops={"arrowstyle": "->",
"connectionstyle": "angle, "
"angleA=0, angleB=100,rad=20"},
fontname=FONT_NAME)
ax.get_children()[ano_x].set_color("C4")
fig.tight_layout()
fig.savefig("./Figs/men_h29.png")
fig, ax = draw_bar(data29[0], data29[2], "C1")
ax.set_title(TITLE + "(H29:女子)", fontname=FONT_NAME)
ano_x = data29[0].index("10~11")
ano_y = data29[2][ano_x]
ax.annotate("平均値を含む階級",
xy=(ano_x, ano_y), xycoords="data",
textcoords="offset points", xytext=(20, 15),
arrowprops={"arrowstyle": "->",
"connectionstyle": "angle, "
"angleA=0, angleB=80,rad=20"},
fontname=FONT_NAME)
ax.get_children()[ano_x].set_color("C3")
fig.tight_layout()
fig.savefig("./Figs/women_h29.png")
性別による比較
H29年度の年金受給権者数の分布を男子と女子で1つのグラフに表すと以下のようになります。
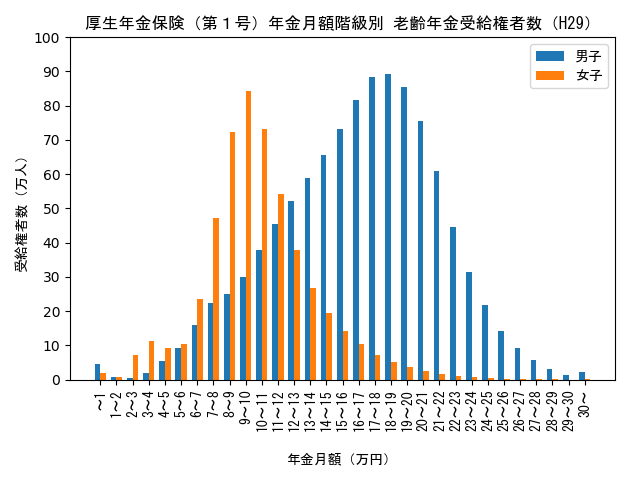
このグラフから、現状では男子と女子の分布に大きな差異があることが分かります。
プログラム
Matplotlibを用いて棒グラフを重ねて描画しています。軸の設定は上記のnenkin_dist.pyをモジュールとして読み込んで利用しています。
# nenkin_dist_gender.py
import numpy as np
from matplotlib import pyplot as plt
import nenkin_reader
import nenkin_dist
def draw_bars(x_labels, y1_values, y2_values, legend1, legend2, color1, color2):
"""棒グラフ作成(2データ)"""
x_ticks = np.arange(len(x_labels))
figure, axis = plt.subplots()
width = 0.35
bar1 = axis.bar(x_ticks - width / 2, y1_values, width, color=color1)
bar2 = axis.bar(x_ticks + width / 2, y2_values, width, color=color2)
nenkin_dist.set_axis(axis, x_labels)
axis.legend((bar1[0], bar2[0]), (legend1, legend2),
prop={'family': nenkin_dist.FONT_NAME, 'size': 10}, loc='best')
return figure, axis
if __name__ == '__main__':
data29 = nenkin_reader.read_xl_table12("./Data/厚年12表_h29年度.xlsx")
fig, ax = draw_bars(*data29, "男子", "女子", "C0", "C1")
ax.set_title(nenkin_dist.TITLE + "(H29)", fontname=nenkin_dist.FONT_NAME)
fig.tight_layout()
fig.savefig("./Figs/men_women_h29.png")
年度による比較
H27年度とH29年度の年金受給権者数の分布を比較すると以下のようになります。
男子のグラフでは、年金月額が10万円前後の受給権者数が減り、15〜20万円付近で増えているのが分かります。
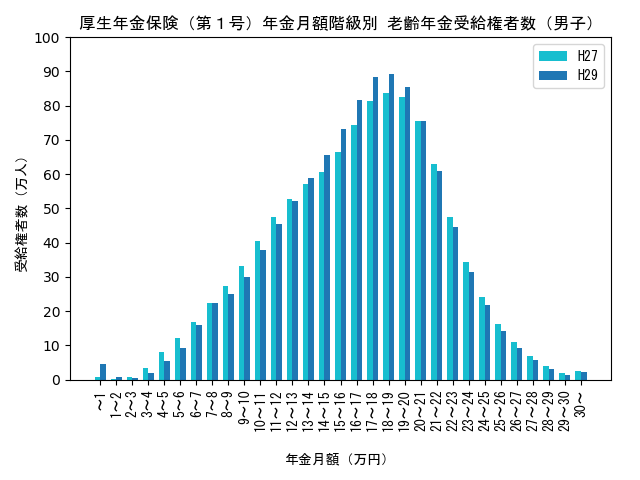
女子のグラフでは、全体に受給権者数が増えていますが、年金月額が9〜12万円付近で特に伸びているのが分かります。
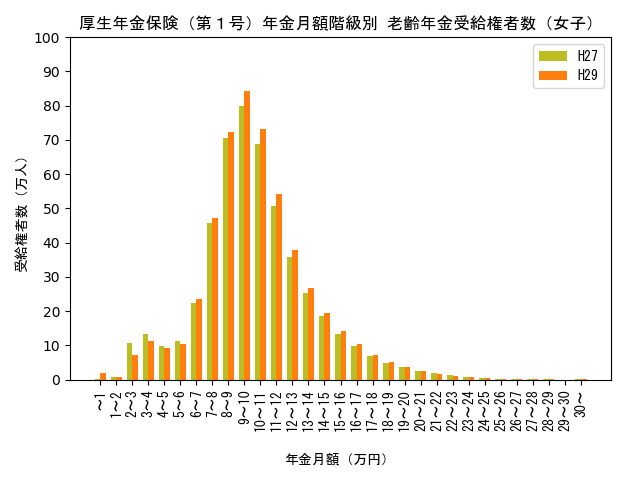
プログラム
上記のnenkin_dist.pyとnenkin_dist_gender.pyを利用して、H27年度とH29年度のデータを1つの棒グラフに描画します。
# nenkin_dist_year.py
import nenkin_reader
import nenkin_dist
import nenkin_dist_gender
data29 = nenkin_reader.read_xl_table12("./Data/厚年12表_h29年度.xlsx")
data27 = nenkin_reader.read_xl_table12("./Data/厚年12表_h27年度.xlsx")
fig, ax = nenkin_dist_gender.draw_bars(data29[0], data27[1], data29[1],
"H27", "H29", "C9", "C0")
ax.set_title(nenkin_dist.TITLE + "(男子)", fontname=nenkin_dist.FONT_NAME)
fig.tight_layout()
fig.savefig("./Figs/men_h29_h27.png")
fig, ax = nenkin_dist_gender.draw_bars(data29[0], data27[2], data29[2],
"H27", "H29", "C8", "C1")
ax.set_title(nenkin_dist.TITLE + "(女子)", fontname=nenkin_dist.FONT_NAME)
fig.tight_layout()
fig.savefig("./Figs/women_h29_h27.png")
まとめ
今回調べた結果から以下のことが分かりました。
- 年金額のバラツキは、所得の格差と比較して抑えられている(変動係数で半分以下)。
- 直近の3年間では、個人が貰える年金額は全般にバラツキが小さくなる傾向にある。
- 女子の年金額は少しずつ増加しているが、性別間の差は未だ歴然である。
以上から年金の最大の課題は、如何に男女間の差を解消するかであると言えます。また、老後の格差は年金ではなく、それ以外の要因で生じることが分かります。例えば、就労、貯蓄、運用などが考えられます。
